VMD-ICA滤波算法
最后更新于:2024-04-07 21:34:04
一、代码运行环境
理论上MATLAB2016以上可以使用,推荐使用MATLAB2020a及更新版本。
二、程序介绍

注: 图标代表该m文件为脚本文件,可以直接运行;
图标代表该m文件为脚本文件,可以直接运行; 图标代表函数文件,在没有输入变量的情况下无法直接运行。更详细的解释可以看这里。
图标代表函数文件,在没有输入变量的情况下无法直接运行。更详细的解释可以看这里。
1.FastICA_25文件夹
第三方FastICA的工具箱,在该代码中调用。工具箱中是FastICA的一些底层实现,该文件夹中的文件不需要修改。当移植代码时,该文件夹需要随其他文件一起移植。
2.demoFilEMDsICA.m文件
进行VMD-ICA滤波的脚本文件,函数filEMDsICA的测试文件,可以直接运行。该脚本中使用的是VMD算法进行分解,当然你可以根据需要换成其他分解程序。程序运行完成后,在MATLAB的工作区,双击reSig变量,可以查看滤波后的具体数值。
运行该文件,将绘制以下图片:

加入噪声前后信号

VMD分解结果

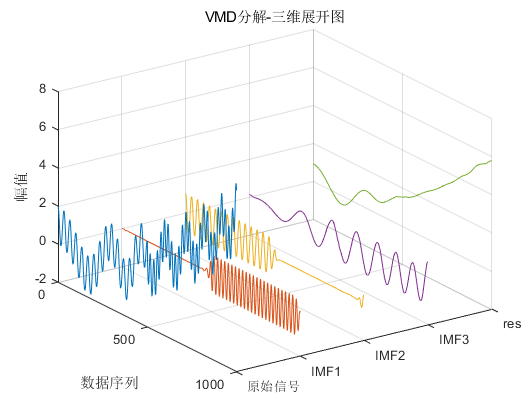
VMD分解三维展开图

FastICA分解结果

滤波效果对比图
另外在命令行窗口将会打印:

3.filEMDsICA.m文件
使用ICA对IMF分量进行处理,并根据信息熵筛选出有效分量进行信号重构。主算法流程全部封装其中。该函数中还包含了求功率谱熵的函数kPowerSpectrumEntropy和求信息熵函数kInformationEntopy。
需注意该函数文件不能直接运行,需参照demoFilEMDsICA的演示案例进行调用。此外需注意,该函数仅对一维数据进行滤波。
function reSig = filEMDsICA(imf)
% filEMDsICA - 使用ICA对IMF分量进行处理,并根据信息熵筛选出有效分量进行信号重构
%
% 输入参数:
% imf - 经过EMD分解得到的IMF分量,每一行为一个IMF分量
%
% 输出参数:
% reSig - 滤波后的信号4.FilterEffectEvaluation.m文件
对滤波效果进行评估。目前包含的评估指标有:信噪比SNR,均方差MSE,波形相似系数NCC。
function [SNR,MSE,NCC] = FilterEffectEvaluation(ori,fil)
% 对滤波效果进行评估
% 目前包含的评估指标有:信噪比SNR,均方差MSE,波形相似系数NCC
% 输入:
% ori:无噪声的原始数据,一维序列
% fil:滤波后的数据,一维序列
% 输出:
% SNR:信噪比
% MSE:均方误差
% NCC:波形相似系数5.pFastICA.m文件
使用FastICA算法分解混合信号并画图的代码。
function [icasig, A, W] = pFastICA(mixedsig, numOfIC, g)
% pFastICA 使用FastICA算法分解混合信号并画图的代码
% 输入:
% mixedsig - 混合信号矩阵,每行代表一个观测值,每列代表一个观测点
% numOfIC - 需要提取的独立成分数目,如果不指定数目,则输入0
% g - 使用的非线性函数类型,可选'pow3', 'tanh', 'gauss'
% Value of 'g': Nonlinearity used:
% 'pow3' (default) g(u)=u^3
% 'tanh' g(u)=tanh(a1*u)
% 'gauss g(u)=u*exp(-a2*u^2/2)
%
% 输出:
% icasig - 分解后的独立成分信号矩阵
% A - 混合矩阵
% W - 解混矩阵
% icasig = W*mixedsig
% mixedsig = A*icasig6.kVMD.m
整合版VMD函数,整合了第三方VMD和MATLAB自带工具箱的VMD分解方法,并且统一输出格式,配合后续进行希尔伯特-黄变换等无缝衔接。
函数参数说明:
function [imf,CenFs] = kVMD(data,FsOrT, alpha, K, tol)
% 整合版VMD函数,整合了第三方VMD和MATLAB自带工具箱的VMD分解方法
% 默认设置下按照MATLAB自带库进行
% 并且统一输出格式,配合后续进行希尔伯特-黄变换等无缝衔接
% 输入:
% data:待分解的数据(一维)
% FsOrT:采样频率或采样时间向量,如果为采样频率,该变量输入单个值;如果为时间向量,该变量为与y相同长度的一维向量。如果未知采样频率,可设置为1
% alpha - 惩罚因子
% K - 指定分解模态数
% tol - 收敛容差,是优化的停止准则之一,可以取 1e-6~5e-6
% 输出:
% imf:内涵模态分量,统一为n*m格式,其中n为模态数,m为数据点数。例如 imf(1,:)即IMF1,imf(end,:)即为残差
% 注意,为了与其他“类EMD”方法分解出来的imf分量保持一致,本程序内将imf排序进行了翻转
% 即保证imf排列是从高频向低频排列
% CenFs:即CentralFrequencies,各imf分量的中心频率
% 注意:使用两种库所得到的imf结果会存在差异,这是由两个库自身算法差异导致的,属于正常现象。7.pVMD.m
封装好的VMD画图程序。
函数参数说明:
function [imf,CenFs] = pVMD(y,FsOrT, alpha, K, tol)
% 画信号VMD分解图
% 输入:
% data:待分解的数据(一维)
% FsOrT:采样频率或采样时间向量,如果为采样频率,该变量输入单个值;如果为时间向量,该变量为与y相同长度的一维向量。如果未知采样频率,可设置为1
% alpha - 惩罚因子
% K - 指定分解模态数
% tol - 收敛容差,是优化的停止准则之一,可以取 1e-6~5e-6
% 输出:
% imf:内涵模态分量,统一为n*m格式,其中n为模态数,m为数据点数。例如 imf(1,:)即IMF1,imf(end,:)即为残差
% 注意,为了与其他“类EMD”方法分解出来的imf分量保持一致,本程序内将imf排序进行了翻转
% 即保证imf排列是从高频向低频排列
% CenFs:即CentralFrequencies,各imf分量的中心频率
% 注意:在使用该代码之前,请务必安装工具箱:https://khsci.com/docs/index.php/2020/04/09/1/画图效果如下(参考):
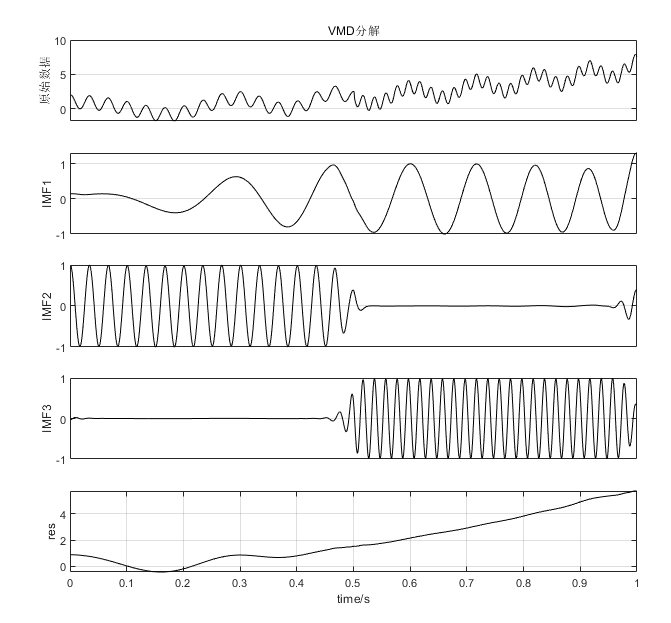
可以同时画出下边这张VMD分解的三维展开图(完整版独有):
三、快速开始
1.运行测试脚本
先在MATLAB里打开下载好的文件夹,然后运行demoFilEMDsICA.m程序,程序运行完毕后如果没报错,且正常画出滤波对比图像,则说明运行环境正常,程序正确。
2.修改仿真数据/导入数据
复制一个demoFilEMDsICA.m的文件副本,在这个副本里做如下修改:
(1)第一种情况,你可能想要对你自己要研究的仿真数据进行滤波测试,此时你需要对 demoFilEMDsICA.m 脚本文件中的第1小节内容进行修改替换即可。需要注意的是,请最好保持变量名的一致,即将无噪声信号命名为ps,添加噪声后的信号命名为x,x和ps都应该是一维数据。此时数据替换完成。
(2)第二种情况,你可能是想对一段真实采集的数据进行滤波,此时需要根据你的文件类型的不同(excel,txt,csv等),将数据导入MATLAB的方法有所不同。同学们可以看博主针对常用文件的导入方法的这个教程,教程上未包含的数据类型,大家可以再参考这个文档。导入完成后请讲这个待滤波信号命名为x。此时你可能没有纯净信号(在大多数实际应用中是没有纯净信号的),这不影响你是用小波阈值滤波进行信号去噪,但是你将无法计算滤波评价指标。
3.替换模态分解方法(可选)
参照 demoFilEMDsICA.m文件中第二步。你可以选择继续使用VMD算法,此时可以根据需要修改alpha、tol、K等参数;你也可以选择替换成其他的模态分解算法,店铺中有相关代码,大家可以在下边链接中找到:https://khsci.com/docs/。至于替换方法,我也录制了视频供大家参考(需完整版)。
4.运行程序
此时运行程序即可。
(需要注意,对于使用真实采集的数据进行滤波,且无纯净信号的情况下,需要删除代码中的第4节滤波评价指标计算,并将第5节滤波对比图像按照注释进行修改)
四、关于完整版与公开版代码
| 功能 | 完整版 | 公开版 |
| 数据导入、参数设置、实现特征提取 | √ | √ |
| 软件全部源码(函数m文件) | √ | × |
| 特征提取数据长度 | 无限制 | 200个点以内 |
| 画图水印 | 无水印 | 有水印 |
| 如何替换其他模态分解方法的视频教程 | √ | × |
五、获取公开版程序(需使用电脑浏览器打开)
ICAfilter公开版代码
注:公开版代码需使用MATLAB2022a及以上版本。
六、获取完整版程序(使用电脑浏览器或者手机浏览器打开)
获取通道一(淘宝):点击此处获取完整版程序
获取通道二(本页面):点击下面“立即支付”按钮,付款后获取完整版代码下载链接和售后联系方式~本通道处于测试阶段,使用该通道可以额外优惠(仅需69元)。付款完成后刷新一下本页面即可看到下载链接。
(注意支付跳转失败的话,请使用浏览器打开本页面)
七、完整版代码重要更新
20240312 完成初版代码
八、常见问题
无。